Notes on Machine Learning
Concepts
Statistical Learning vs Machine Learning
Different goals:
Statistical Learning: inference and generalization
Machine Learning: maxmize prediction
Machine learning is the science of getting computers to act without being explicitly programmed. - Andrew Ng
Field of study that gives computers the ability to learn without being explicitly programmed. -Arthur Samuel, IBM, 1959
Model
Common form: \(y = f(x) + \epsilon\); Interested in estimating functional form of f(x)
Approaches: parametric; non=parametric estimation
Selecting and fitting a model
Flexible models vs. inflexible models
Flexibility is a measure of how much a fitted model can vary with a given data.
-
Example of flexible models (high variance, low bias): splines, 10 degree curve, Support Vector Machines
-
Example of inflexible models (low variance, high bias): linear regression
-
When a inflexible model is preferred:
-
interpretablility: understand how the explanatory variables affect the response variable
-
a small e size (small n) and large number of predictors (large p)
-
the variance of the error terms, i.e. \(sigma^{2}=Var(\epsilon)\), is extremely high
-
-
When a flexible model is preferred:
-
a large sample size (large n) and small number of predictors (small p)
-
relationship between the predictors and response is highly non-linear
-
A flexible model will cause you to fit too much of the noise in the problem (when variance of the error terms is high).
Error
Error = Irreducible Error + \(Bias^2\) + Variance
Error/ Bias / Variance
Bias
Error caused by choosing an algorithm that cannot accurately model the signal in the data, i.e. the model is too general or was incorrectly selected. For example, selecting a simple linear regression to model highly non-linear data would result in error due to bias.
Variance
Error from an estimator being too specific and learning relationships that are specific to the training set but do not generalize to new samples well. Variance can come from fitting too closely to noise in the data, and models with high variance are extremely sensitive to changing inputs. Example: Creating a decision tree that splits the training set until every leaf node only contains 1 sample.
Irreducible error
error caused by noise in the data that cannot be removed through modeling. Example: inaccuracy in data collection causes irreducible error.
Bias-variance tradeoff
trade-off between underfitting and overfitting
From simple to complex models, flexibility increases, variance increases, bias decreases.
As you decrease variance, you tend to increase bias. As you decrease bias, you tend to increase variance.

Metrics for evaluating models
“No Free Lunch Theorem”
TPR/FPR/TNR/FNR
Optimization Methods
-
Netwon’s method
-
Quasi-Newton methods (ex. LBFGS)
-
Gradient Descent
Overfitting
When a model makes much better predictions on known data (data included in the training set) than unknown data (data not included in the training set); High variance, low bias; Flexible model
Combate overfitting:
- simplify the model by use fewer parameters
- simply the model by changing the hyperparameters
- simplify the model by introducing regularization
- select a different model
- use more training data
- gather better quality data
Hyper-parameter tuning
Resampling Methods
-
Essential to test and evaluate statistical models
-
Repeatedly draw from your original sample to obtain additional information about the model
Encoding categorical data
-
Label encoding (non-ordinal) - each category is assigned a numeric value not representing any ordering. Example: [red, blue, green] could be encoded to [8, 5, 11].
-
Label encoding (ordinal) - each category is assigned a numeric value representing an ordering. Example: [small, medium, large] could be encoded to [1, 2, 3]
-
One-hot encoding - each category is transformed into a new binary feature, with all records being marked 1/True or 0/False. Example: color = [red, blue, green] could be encoded to color_red = [1, 0, 0], color_blue = [0, 1, 0], color_green = [0, 0, 1]
Train and testing set
-
training set is used for model construction (can be reused many times to build different models)
-
test set is used to evaluate the performance of the final model (can be used only once)
Validation
-
Intuition: fit the model and evaluate it many times on the same data
-
Method: split half of the training data as validation set
-
Drawback: validation estimates of the test error rates can be highly variable depending on which observations are sampled into the training and validation sets (ex. outliers in the validation sets)
Cross-validation
for evaluating a model’s performance relative to other models
- LOOCV: leave-one-out cross validation
only remove one observation for the validation set, and keep all remaining observations in the training set
\[CV_N = {\frac{1}{N}}{\sum_{i=1}^{N}}MSE_i\]-
Pro: unbiased compared to naive 1-stage validation approach
-
Pro: highly flexible and works with any kind of predictive modeling
-
Cro: high variance because the N “training sets” are so similar to one another;
-
Cro: computationally expensive
- K-fold cross-validation: divides the observations into K folds of approximately equal size
Typical K= 5 or 10; Random sampling without replacement
\[CV_K = \frac{1}{K}\sum_{i=1}^{K}MSE_i\]-
Pro: less variance in test error estimate compared with LOOCV
-
Cro: leads to a slight increase in usually bias
- Other validations
-
Stratified cross-validation
-
Repeated cross-validation
-
Cross-validation with time series data
Bootstrapping
non-parametric measure of the accuracy of a parameter estimate or method
Purpose: quantify uncertainty associated with some estimator
Loss
-
MSE/Sum of squared errors
-
Cross-entropy
-
Kullback-Leibler (KL) divergence
-
Gini impurity for decision tree
-
Information gain
Estimators of errors
adjusting the training error to penalize additional features
Mallows’s Cp
\(C_{p} = \frac{1}{n}(RSS+2d hat{\sigma}^2)\) Wiki
AIC
\[AIC=AIC = −2logL + 2 × d\]In the linear model, \(−2LogL = \frac{RSS}{hat{\sigma}^2)}\)
BIC
\[BIC = \frac{1}{n}(RSS+log(n) * hat{\sigma}^2)\](imposes harsher penalty on models with more features, resulting in selection of less complex models)
Adjusted R^2
\[Adjust R^2 = 1-\frac{RSS/(n-d-1)}{TSS/(n-1)}\]1SE Rule
The rule suggests to not necessarily choose the model with minimum error, but to choose the simplest model within one SE of the min error.
Data Preparation
-
Cleaning/Pre-processing
-
Missing data
-
Unbalanced data
How to fix an Unbalanced Dataset@KDnuggets
Resampling strategies for imbalanced datasets@Kaggle
Diving Deep with Imbalanced Data@Datacamp
-
Feature engineering
-
Feature selection
-
Effective sample size
-
Time correaltions
-
backward
-
forward
-
subset
-
L1
-
L2
-
PCA
Ensemble learning
-
Bagging
-
Boosting
-
Xgboost
-
xgboost vs DT
-
xgboost vs RF
-
xgboost vs boosting
Estimation Methods
-
MLE / MAP
-
Expectation-Maxmization algorithm
Occam’s Razor
“the simplest solution is most likely the right one”
“when presented with competing hypotheses that make the same predictions, one should select the solution with the fewest assumptions”
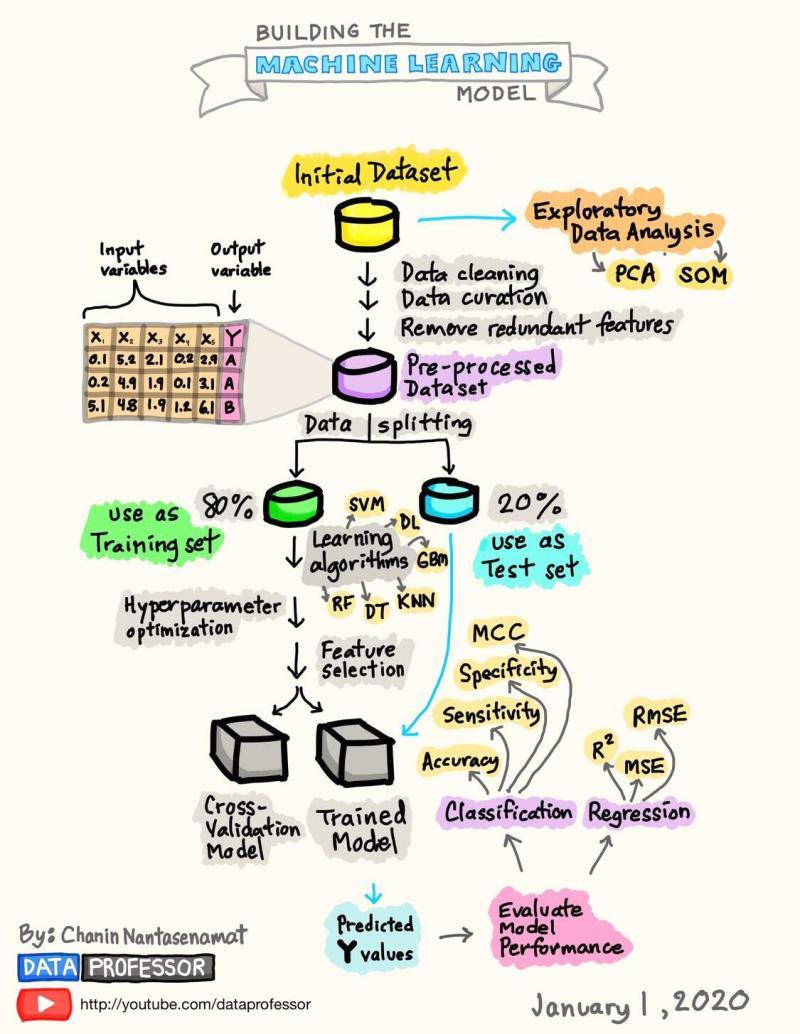
Building ML Model
Model parameter v.s. Learning hyperparameter
-
Model parameters are the rules that mathematically describe the final model that makes predictions, such as slopes or intercept in a linear regression model.
-
Learning hyperparameter describes the way in which a model parameter is learned and settings for training the model, e.g. learning rate, penalty terms, number of features to include in a weak predictor, etc.
Model parameters: determined/fitted using the training data set
Hyperparameters: adjustable parameters to be tuned for optimal performance
Supervised Machine Learning
Regression
Linear Model
Two assumptions: 1. Linear; 2. Additive (unit changes)
The coefficients in a least squares model typically are interpreted as the expected change in the outcome of interest associated with a unit change in the predictors, \(Y = \beta_{0}+\beta_{1}X_{1}+...+\beta_{p}X_{p}+\epsilon\)
- Unconditional marginal effects are the expected change in Y associated with a unit change in X (partial derivative), \(\frac{\partial Y}{\partial X_{1}} = \beta_{1}\)
(constant values where we are directly observing the change in slope of Y, given X)
- Conditional marginal effects are the expected change in Y associated with a unit change in X (partial derivative), such as \(\frac{\partial Y}{\partial X_{1}} = \beta_{1}+\beta_{2}X_{1}\) or \(\frac{\partial Y}{\partial X_{1}} = \beta_{1}+2\beta_{2}X_{1}\)
3 types of marginal effects:
-
Marginal effects at representative values (MERs) - MFX at a particularly interesting combination of X values
-
Marginal effects at means (MEMs) - MFX of each feature at the means of the others
-
Average marginal effects (AMEs) - MFX at every observed value of X, averaged across the effect estimates
(a single quantity summary that reflects the full distribution of X as observed in the sample )
OLS (ordinary least squares)
Linear model selection
-
Linearity
-
Correlation vs Causality
-
Multicollinearity
-
Interaction variables (ex. x1*x2)
-
Normality
-
Homoscedasticity
-
Monotonic relationship
Shrinkage/Regularization
shrinkage employs a technique to constrain or regularize the coefficient estimates
can significantly reduce their variance, and ultimately the error in the model, resulting in stronger predictions
- Ridge
estimates the coefficients that minimize \(RSS + \lambda \sum_{j=1}^{p} {\beta_{j}}^2\)
where \(\lambda\) is a tuning parameter, which is the penalty we are imposing on the estimates
-
Lasso
-
Elastic-net
Bayesian linear regression
Local regression
Generalized additive model
Logistic regression
K-Nearest regression
kNN regression uses a moving average to generate the regression line
Given a value for \(K\) and a prediction point \(x_{0}\), kNN regression identifies the \(K\) training observations nearest to the prediction point \(x_{0}\), represented by \(N_{0}\)
Estimates \(f(x_{0})\) as the average of all the training responses in \(N_{0}\), \(\hat{f(x_{0})} = \frac{1}{K}\sum_{x_{i}∈N_{0}}^{}y_{i}\)
-
When K is small, flexible, low bias but high variance
-
When K is large, inflexible, low variance but higher bias
KNN erforms worse as the number of predictors p increases.
Application in marketing: likealike model
Non-Linear Estimation
-
Polynomial regression: adding additional predictors obtained by raising each to a power
-
Step function: split the range of a feature into k regions and fits a piecewise constant function
-
Regression splines: polynomials + step functions that provide more flexibility; split the range of X into k distinct regions and within each region, fit a polynomial function
-
Smoothing splines: smoothing splines result from minimizing an RSS criterion subject to a smoothness penalty
-
Local regression: regions are allowed to overlap to allow for improved smoothness
-
Generalized additive models: multiple predictors
Classification
Task:
-
Build a function C(X) that takes the feature vector X and predicts its value for Y , i.e. C(X) ∈ C
-
Classify observations as a function of some vector of features
-
Model the probability that Y belongs to a particular category instead of Y directly
Threshold: f(X)>=0.5, \(\hat{Y}=1\); f(X)<0.5, \(\hat{Y}=1\)
Odds
Probability of one outcome divided by the probability of the other outcome \(\frac{}{}\)
Key terms: Sensitivity_and_specificity

Purpose: categorize all the variables that form the output
Softmax classifier
K-nearest neighbors
Naïve bayes
Support vector machine
Evaluation metrics for classification
- Accuracy
measures the percentage of the time you correctly classify samples: (true positive + true negative) / all samples
- Precision
measures the percentage of the predicted members that were correctly classified: true positives / (true positives + false positives)
- Recall
measures the percentage of true members that were correctly classified by the algorithm: true positives / (true positives + false negative)
- F1
measurement that balances accuracy and precision (or you can think of it as balancing Type I and Type II error)
- AUC
Area Under The Curve—represents degree or measure of separability
describes the probability that a classifier will rank a randomly chosen positive instance higher than a randomly chosen negative one
- ROC
Receiver Operating Characteristics—probability curve
- Gini
a scale and centered version of AUC
- Log-loss
similar to accuracy but increases the penalty for incorrect classifications that are “further” away from their true class. For log-loss, lower values are better.
Source: Kyle McKiou Blog
Non-parametric regression
How: can divide X into many narrow intervals just like we would for a histogram and estimate the conditional distribution of Y and estimate the conditional mean of Y within each bin
Bottom line: Unless your dataset is extremely large or you have a small handful of variables with a low number of unique values, naive nonparametric estimation will not be effective
K-Nearest classification
Similar to kNN regression, given a positive integer K and a test observation x0, the kNN classifier identifies the K nearest training observations to x0, represented by N0.
The conditional probability for class j is the fraction of points in \(N_{0}\) whose response values equal j, \(Pr(Y = j|X = x_{0}) = \frac{1}{K}\sum_{x_{i}∈N_{0}}^{} I(y_{i}=j)\)
where I is an indicator variable that equals 0 for correct classification and equals 1 for incorrect classification
Bayes decision boundary
For classification problems, the test error rate is minimized by a simple classifier that assigns each observation to the most likely class given its predictor values, \(Pr(Y = j|X = x_{0})\) where \(x_{0}\) is the test observation and each possible class is represented by J
(conditional probability that Y = j, given the observed predictor vector \(x_{0}\))
The Bayes classifer produces the lowest possible test error rate, called the Bayes error rule, because it will always assign observations based on the maximum conditional probability, \(1 − E(\underset{j}{\operatorname{max}} Pr(Y = j|X))\) where the expectation averages the probability over all possible values of X
Naive Bayes
Bayes Theorem: By combining our observed information, we update the prior information on probabilities to compute a posterior probability that an observation belongs to class Ck, \(Posterior = \frac{Prior × Likelihood}{Evidence}\)
The Naive Bayes assumes the predictors are conditionally independent of one another
For continuous predictors, we typically make an additional assumption of normality so that we can use the probability from the probability density function (PDF).
Discriminant analysis (LDA, QDA)
Packages & Tools
Lime: Explaining the predictions of any machine learning classifier
Regression vs Classification
Different y:
Regression: response is quantitative (continuous)
Classification: response is qualitative (binary/multinomial)
Tree-based Methods
Classification trees
Boosted regression trees
Random forests
GBDT: Gradient Boosting Decision Tree
GBDT loss fucntion
Unsupervised Machine Learning
Exploratoty data analysis
Visualization
-
Histograms
-
Boxplot
-
t-SNE
Factor analysis
Discriminant analysis
Clustering
-
Distance
-
Clusterability
-
Kmeans
-
Hard partitioning
-
Soft partitioning
-
Hierarchical clustering
-
Gaussian mixture models
Association rule mining
Dimensionality reduction
TO solve problems such as multicollinearity, overfitting, and curse of dimensionality
Principal component analysis
Objective: transform the predictors and then fit a least squares model using the transformed variables instead of the original predictors
\[Z_m = \sum_{j=1}^p \varphi_jm X_j\]-
uses an eigen decomposition to transform the original data into linearly independent eigenvectors
-
most important vectors (with highest eigenvalues) are then selected to represent the features in the transformed space
Non-negative matrix factorization (NMF)
- can be used to reduce dimensionality for certain problem types while preserving more information than PCA
Embedding techniques
- various embedding techniques, e.g. finding local neighbors as done in Local Linear Embedding, can be used to reduce dimensionality
Clustering or centroid techniques
- each value can be described as a member of a cluster, a linear combination of clusters, or a linear combination of cluster centroids
Source: Kyle McKiou
Natural Language Processing
Text Mining
Text mining is the process of examining large collections of text and converting the unstructured text data into structured data for further analysis like visualization and model building.
Word Embedding
“training a model with a neural network auto-encoder (one of Google’s word2vec algorithms) that best describes corpus words in their local linguistic contexts, and exploring their locations in the resulting space to learn about the discursive culture that produced them” (Computational COntent Analysis class HW6 Tutorial)
Gensim: Store and query word vectors
BERT
Pre-processing
Sentiment Analysis
Topic Models
-
LDA/Gibbs
-
Structural
-
Non-negative factorization
Tutorials
Topic Modelling in Python with NLTK and Gensim
TextBlob: Simplified Text Processing
Analyzing Customer reviews using text mining to predict their behaviour Hidden Markov Chain
Knowledge graph
Graph theory + Network Science + NLP —> Better search result with multiple sources
Python tutorial: how-to-build-knowledge-graph-text-using-spacy
Companies:
HopHR Knowledge Graph Data Scientist
Papers:
A Review of Relational Machine Learning for Knowledge Graphs
Application: Chatbox
Ex: Return ngrams
Q: write a function to return ngram(string,n) eg: ngram(“abc”,2) —> [“a”,”b”,”c”,”ab”,”bc”]
Text Summarization
Towards DS: Text Summarization with Amazon Reviews
Reinforcement Learning
Purpose: max the performance of the machine in a way that helps it to grow
GAN
Deep Learning
Book by Amazon Scientists: Dive into Deep Learning
Single layer and multi-layer perceptron neural nets
Convolutional Neural Network
Recursive Neural Network
Self-organizing maps
Dropout
Batch Normalization
Back propagation
Keras
Tensorflow
Recommendation Systems
Collaborative Filtering
Information Retrieval
Search/Display
Ads retrieval and recommendation
Spam-traffic and click-farm detection
Infrastructure development
Traffic and revenue prediction
Ads pricing
Audience expansion
Links to online resources
An Introduction to Statistical Learning
The Elements of Statistical Learning (2nd edition)
Interpretable Machine Learning
Understanding Machine Learning: From Theory to Algorithms
CS231n Convolutional Neural Networks for Visual Recognition
Unofficial Google Colaboratory Notebook and Repository Gallery
Awesome Machine Learning Jupyter Notebooks for Google Colaboratory
Toronto CSC401/2511: Natural Language Computing
| [Stanford CS224N: NLP with Deep Learning | Winter 2019](https://www.youtube.com/playlist?list=PLoROMvodv4rOhcuXMZkNm7j3fVwBBY42z) |
| [Stanford CS231n: Convolutional Neural Networks for Visual Recognition | Spring 2019](http://cs231n.stanford.edu/) |
| [Toronto CSC 421/2516: Neural Networks and Deep Learning | Winter 2019](https://www.cs.toronto.edu/~rgrosse/courses/csc421_2019/) |
Machine Learning Interview Questions

Leave a Comment